KOMPOSISI FUNGSI DAN INVERS FUNGSI

-

 

Fungsi Komposisi

Seperti yang tela disebutkan di atas, fungsi komposisi merupakan suatu penggabungan dari suatu operasi dua jenis fungsi f(x) dan juga g(x) sehingga mampu menghasilkan suatu fungsi baru.

Adapun rumus untuk fungsi komposisi, yaitu:

Rumus Fungsi Komposisi

Sperti yang terdapat pada uraian di atas, operasi untuk fungsi komposisi tersebut biasa dinotasikan dengan penggunakan huruf atau simbol “o”.

Di mana simbol tersebut bisa kita baca sebagai komposisi ataupun bundaran. Fungsi baru inilah yang bisa terbentuk dari f(x) dan g(x) yaitu:

1. (f o g)(x) yang berarti g dimasukkan ke f

2. (g o f)(x) yang berarti f dimasukkan ke g

Fungsi tunggal merupakan suatu fungsi yang dapat dinotasikan dengan penggunakan huruf “f o g” atau dapat dibaca “f bundaran g”.

Lalu Fungsi (f o g) (x) = f (g (x)) → fungsi g (x) dikomposisikan sebagai fungsi f (x)

Sementara itu, “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan fungsi f yang diselesaikan terlebih dahulu dari fungsi g.

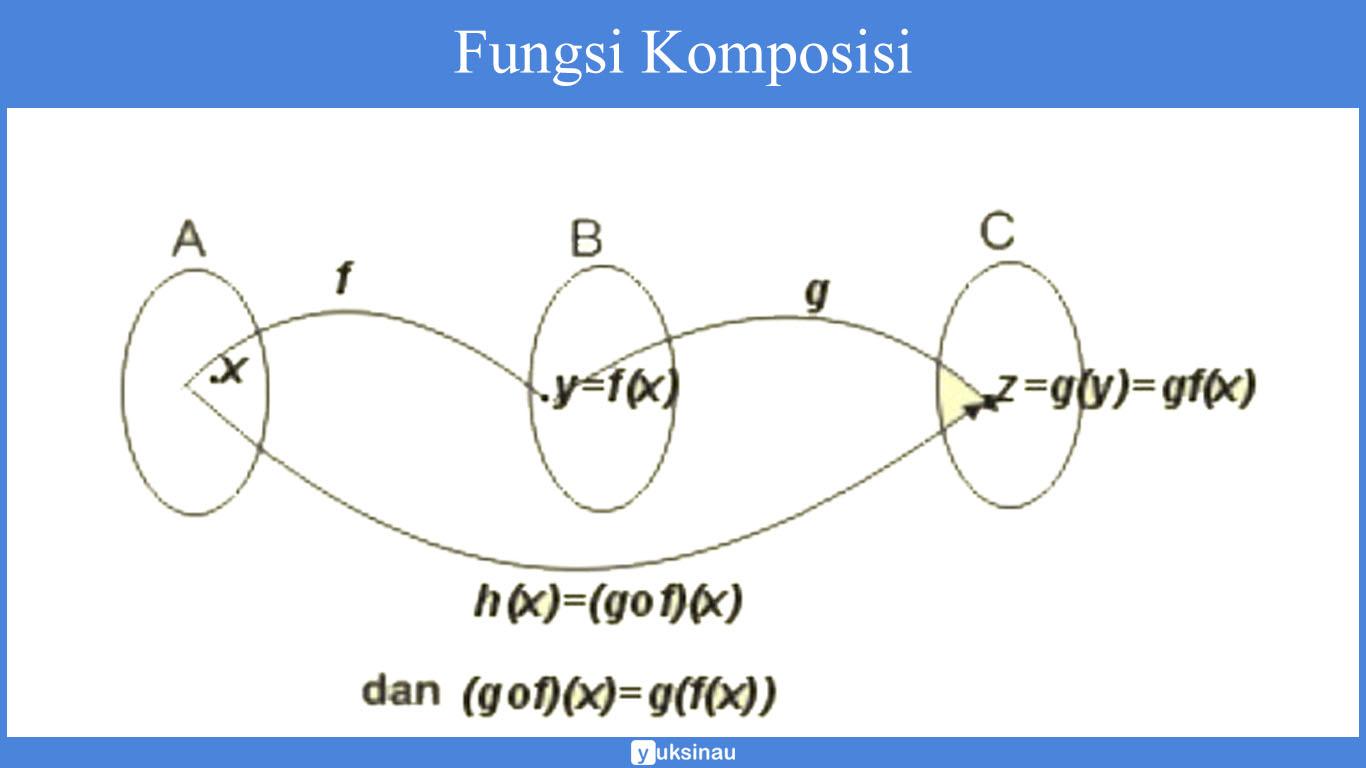
Agar dapat memahami fungsi ini, perhatikan gambar dibawah ini :

fungsi komposisi f o g o h

Advertisement

Dari skema rumus di atas, dapat kita ketahui bahawa:

Apabila f : A → B ditentukan dengan menggunakan rumus y = f(x)

Apabila g : B → C ditentukan dengan menggunakan rumus y = g(x)

Sehingga, akan kita peroleh hasil fungsi g dan f yaitu:

h(x) = (gof)(x) = g( f(x))

Dari definisi di atas maka bisa kita simpulkan jika fungsi yang melibatkan fungsi f dan g bisa kita tulis seperti berikut ini:

  • (g o f)(x) = g(f(x))
  • (f o g)(x) = f(g(x))

Komentar

Posting Komentar

Postingan populer dari blog ini

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU

-
Gambar
  Perbandingan Trigonometri dari Suatu Sudut pad aSegitiga Siku-Siku Segitiga siku-siku yaitu segitiga dengan salah satu sudutnya adalah  . Dalam segitiga siku-siku terdapat sisi miring yang disebut hipotenusa. Kuadrat hipotenusa yaitu jumlah dari kuadrat dua sisi lainnya. Secara sistematis, teorema Pythagoras dapat dinyatakan sebagai berikut. dengan  a  dan  b  adalah sisi siku-siku dan  c adalah sisi miringnya. Untuk lebih jelasnya maka perhatikan gambar berikut. Perbandingan Sinus (sin), Cosinus (cos), Tangen (tan), Cosecan (scs), Secan (sec), dan Cotangen (cot). Untuk mengetahui rasio trigonometri, kita menggunakan segitiga siku-siku. Untuk itu, kita harus mengetahui letak sisi depan, sisi samping, dan sisi miring. Untuk lebih jelasnya perhatikan gambar berikut: Sisi Miring adalah sisi di depan sudut siku-siku. Sisi Depan adalah sisi di depan sudut α. Sisi Samping adalah sisi siku-siku lainnya.   Setelah mengetahui sisi miring, sisi depan, dan...
Baca selengkapnya

SISTEM PERTIDAKSAMAAN KUADRAT-LINEAR DAN BEBERAPA CONTOH SOALNYA

-
  Keliling sebuah persegi panjang sama dengan 20 cm. Jika luas persegi panjang itu tidak kurang dari 21 cm 2 , maka tentukanlah batas-batas nilai panjang dari persegi panjang tersebut. Jawab ■   Misalkan panjang dan lebar persegi panjang tersebut adalah x cm dan y cm. Maka keliling persegi panjang adalah K = 2(x + y) = 20 ⇔  2(x + y) = 20 ⇔  x + y = 10 ⇔  y = 10  –  x Luas persegi panjang adalah adalah L = x . y ⇔  L = x(10  –  x) ⇔  L = 10x  –  x 2 ■   Dari soal telah ditentukan bahwa luas persegi panjang tidak kurang dari 21 cm 2 , hal ini berarti L  ≥  21 sehingga ⇔  10x  –  x 2   ≥  21 ⇔  10x  –  x 2   –  21  ≥  0 (kita ubah  – x 2  menjadi x 2  dengan mengali kedua ruas dengan -1) ⇔  x 2   –  10x + 21  ≤  0 (jika kedua ruas dikali dengan bilangan negatif, maka tanda berubah) ⇔  (x  –  3)(x...
Baca selengkapnya

SOAL FUNGSI: KUADRAT, RASIONAL, IRASIONAL

-
Gambar
  Contoh 1 Tentukan daerah asal atau domain dari fungsi rasional di bawah ini Penyelesaian Kita lihat penyebut dari fungsi rasional ( pecahan ) di atas adalah x + 1. Dan seperti yang kita ketahui bahwa supaya pecahan tersebut mempunyai nilai bilangan real maka penyebut tidak boleh bernilai 0. Sehingga x + 1 ≠ 0 x ≠  – 1 Jadi Df : { x | x ∈ R, dan x ≠  – 1 } Baca Juga :     LATIHAN SOAL PERSIAPAN PTS 2 MAT PEM Contoh 2 Tentukan daerah asal atau domain dari fungsi rasional di bawah ini Penyelesaian Kita lihat penyebut dari fungsi rasional ( pecahan ) di atas adalah x² -3x + 2. Dan seperti yang kita ketahui bahwa supaya pecahan tersebut mempunyai nilai bilangan real maka penyebut tidak boleh bernilai 0. Sehingga x² -3x + 2 ≠ 0  kita faktorkan (x – 1)(x – 2) ≠ 0 x – 1 ≠ 0 atau  x – 2 ≠ 0 maka x ≠ 1  atau x ≠ 2 Jadi Df : { x | x ∈ R, dan x ≠ 1 atau  x ≠ 2 } Menentukan daerah asal fungsi irasional Contoh 1 Tentukan daerah asal atau domain dari...
Baca selengkapnya