fungsi linear dan kuadrat

-

 1). Pengertian fungsi linier

Fungsi linier adalah suatu fungsi yang variabelnya berpangkat satu atau suatu fungsi
yang grafiknya merupakan garis lurus. Oleh karena itu fungsi linier sering disebut
dengan persamaan garis lurus (pgl) dengan bentuk umumnya sbb.:

f : x → mx + c atau

f(x) = mx + c atau
y = mx + c
m adalah gradien / kemiringan / kecondongan dan
c adalah konstanta2). Melukis grafik fungsi linier
Langkah-langkah melukis grafik fungsi linier
a Tentukan titik potong dengan sumbu x, y = 0 diperoleh koordinat A( x1, 0)
b Tentukan titik potong dengan sumbu y, x = 0 diperoleh koordinat B( 0, y1)
c hubungkan dua titik A dan B sehingga terbentuk garis lurusPersamaan linier juga dapat ditulis ditulis dengan simbol y = ax + b (ini untuk memudahkan kita dalam memahami gambar)Jika b bernilai positif : fungsi linier digambarkan garis dari kiri bawah ke kanan atas
Jika b bernilai negatif : fungsi linier digambarkan garis dari kiri atas ke kanan bawah
Jika b bernilai nol : digambarkan garis yg sejajar dengan sumbu datar x


Gambar Fungsi Linear
Apabila b bernilai negatif : Y = 10 – 2X maka kurva bergerak dari kiri atas ke kanan bawah


Apabila b bernilai positif : Y = 2 + 2X maka kurva bergerak dari kiri bawah ke kanan atas


3). Gradien dan persamaan garis lurus
a). Garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien m:
m = y1-y2 atau m = y2-y1
x1-x2 x2-x1b. Persamaan garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) adalah:
y-y1 = x-x1
y2-y1 x2-x1c. Persamaan garis lurus (pgl) yang bergradien m dan melalui titik A(x1, y1) adalah:
y = m (x – x1 ) + y14). Menentukan gradien dari persamaan garis lurus (pgl)
@ Persamaan garis lurus : ax + by = c maka gradiennya m = – a/b
@ Persamaan garis lurus : y = ax + b maka m = a
@ Garis yang sejajar sumbu x memiliki persamaan y = c dan m = 0
@ Garis yang sejajar sumbu y memiliki persamaan x = c dan tidak memiliki gradient

5). Titik potong dua buah garis
Menentukan titik potong dua buah garis lurus identik dengan menyelesaikan
penyelesaian sistem persamaan linier dua variabel baik dengan metode eleminiasi,
metode substitusi maupun metode grafik

6). Hubungan dua buah garis
Dua garis yang bergradien m1 dan m2 dikatakan sejajar jika m1 = m2 dan tegak lurus jika m1 x m2 = -1

Berimpit
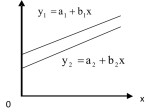
Dua garis lurus akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari garis yang lain. Dengan demikian , garis akan berimpit dengan garis , jika

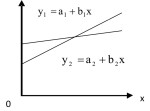
Sejajar
Dua garis lurus akan sejajar apabila lereng/gradien garis yang satu sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis akan sejajar dengan garis , jika

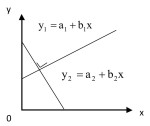
Berpotongan
Dua garis lurus akan berpotongan apabila lereng/gradien garis yang satu tidak sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis akan berpotongan dengan garis , jika

Tegak lurus
Dua garis lurus akan saling tegak lurus apabila lereng/gradien garis yang satu merupakan kebalikan dari lereng/gradien dari garis yang lain dengan tanda yang berlawanan. Dengan demikian , garis akan tegak lurus dengan garis , jika atau

Komentar

Posting Komentar

Postingan populer dari blog ini

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU

-
Gambar
  Perbandingan Trigonometri dari Suatu Sudut pad aSegitiga Siku-Siku Segitiga siku-siku yaitu segitiga dengan salah satu sudutnya adalah  . Dalam segitiga siku-siku terdapat sisi miring yang disebut hipotenusa. Kuadrat hipotenusa yaitu jumlah dari kuadrat dua sisi lainnya. Secara sistematis, teorema Pythagoras dapat dinyatakan sebagai berikut. dengan  a  dan  b  adalah sisi siku-siku dan  c adalah sisi miringnya. Untuk lebih jelasnya maka perhatikan gambar berikut. Perbandingan Sinus (sin), Cosinus (cos), Tangen (tan), Cosecan (scs), Secan (sec), dan Cotangen (cot). Untuk mengetahui rasio trigonometri, kita menggunakan segitiga siku-siku. Untuk itu, kita harus mengetahui letak sisi depan, sisi samping, dan sisi miring. Untuk lebih jelasnya perhatikan gambar berikut: Sisi Miring adalah sisi di depan sudut siku-siku. Sisi Depan adalah sisi di depan sudut α. Sisi Samping adalah sisi siku-siku lainnya.   Setelah mengetahui sisi miring, sisi depan, dan...
Baca selengkapnya

SISTEM PERTIDAKSAMAAN KUADRAT-LINEAR DAN BEBERAPA CONTOH SOALNYA

-
  Keliling sebuah persegi panjang sama dengan 20 cm. Jika luas persegi panjang itu tidak kurang dari 21 cm 2 , maka tentukanlah batas-batas nilai panjang dari persegi panjang tersebut. Jawab ■   Misalkan panjang dan lebar persegi panjang tersebut adalah x cm dan y cm. Maka keliling persegi panjang adalah K = 2(x + y) = 20 ⇔  2(x + y) = 20 ⇔  x + y = 10 ⇔  y = 10  –  x Luas persegi panjang adalah adalah L = x . y ⇔  L = x(10  –  x) ⇔  L = 10x  –  x 2 ■   Dari soal telah ditentukan bahwa luas persegi panjang tidak kurang dari 21 cm 2 , hal ini berarti L  ≥  21 sehingga ⇔  10x  –  x 2   ≥  21 ⇔  10x  –  x 2   –  21  ≥  0 (kita ubah  – x 2  menjadi x 2  dengan mengali kedua ruas dengan -1) ⇔  x 2   –  10x + 21  ≤  0 (jika kedua ruas dikali dengan bilangan negatif, maka tanda berubah) ⇔  (x  –  3)(x...
Baca selengkapnya

SOAL FUNGSI: KUADRAT, RASIONAL, IRASIONAL

-
Gambar
  Contoh 1 Tentukan daerah asal atau domain dari fungsi rasional di bawah ini Penyelesaian Kita lihat penyebut dari fungsi rasional ( pecahan ) di atas adalah x + 1. Dan seperti yang kita ketahui bahwa supaya pecahan tersebut mempunyai nilai bilangan real maka penyebut tidak boleh bernilai 0. Sehingga x + 1 ≠ 0 x ≠  – 1 Jadi Df : { x | x ∈ R, dan x ≠  – 1 } Baca Juga :     LATIHAN SOAL PERSIAPAN PTS 2 MAT PEM Contoh 2 Tentukan daerah asal atau domain dari fungsi rasional di bawah ini Penyelesaian Kita lihat penyebut dari fungsi rasional ( pecahan ) di atas adalah x² -3x + 2. Dan seperti yang kita ketahui bahwa supaya pecahan tersebut mempunyai nilai bilangan real maka penyebut tidak boleh bernilai 0. Sehingga x² -3x + 2 ≠ 0  kita faktorkan (x – 1)(x – 2) ≠ 0 x – 1 ≠ 0 atau  x – 2 ≠ 0 maka x ≠ 1  atau x ≠ 2 Jadi Df : { x | x ∈ R, dan x ≠ 1 atau  x ≠ 2 } Menentukan daerah asal fungsi irasional Contoh 1 Tentukan daerah asal atau domain dari...
Baca selengkapnya